Benchmark Description
Design principles
Our benchmark is organized with three design principles.
conceptually pure blocks: We test one basic principle of intuitive physics at a time (see Test_Blocks for details).
minimal set design: Possible and impossible videos are constructed in carefully matched sets, in order to avoid bias.
parametric design: Task difficulty is controlled by manipulating the duration of occlusion, number and movement of the objects.
We illustrate the minimal set design on the Block 1 (object permanence), which tests the principle that macroscopic objects either exist or not, but they do not flip in and out of existence, even when we don’t look at them. It is a very important principle, that has a lot of applications in real life (does the car hidden by the truck still exists?).
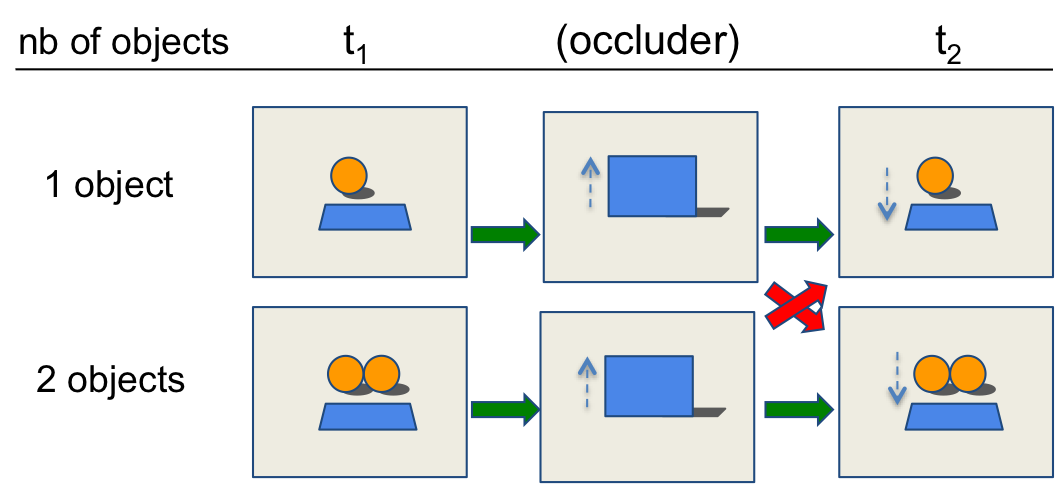
To test for object permanence, we construct four movies. The first two correspond to following the green arrows: the movie starts with one (two) object(s) presented on an empty background, then a screen is raised, totally occluding the object(s) for a period of time, then the screen is lowered, revealing the object(s) in its/their original position(s). The two impossible movies correspond to following the red arrows: it starts with one object and ends up with two, or vice versa. The two possible and two impossible movies are therefore composed of exactly the same frames and pixels, the only difference between them being the particular sequence of events which is in the first two cases compatible and in the last two incompatible with the principle of object permanence.




The test samples therefore come as quadruplets: 2 possible cases and 2 impossible ones. They are organized into 18 conditions resulting from the combination of 2 visibilities (visible vs occluded) times 3 numbers of objects (0 vs 1, 1, vs 2, 2 vs 3) and 3 mouvements types (static, dynamic 1, dynamic 2) as follows (still for Block 1):
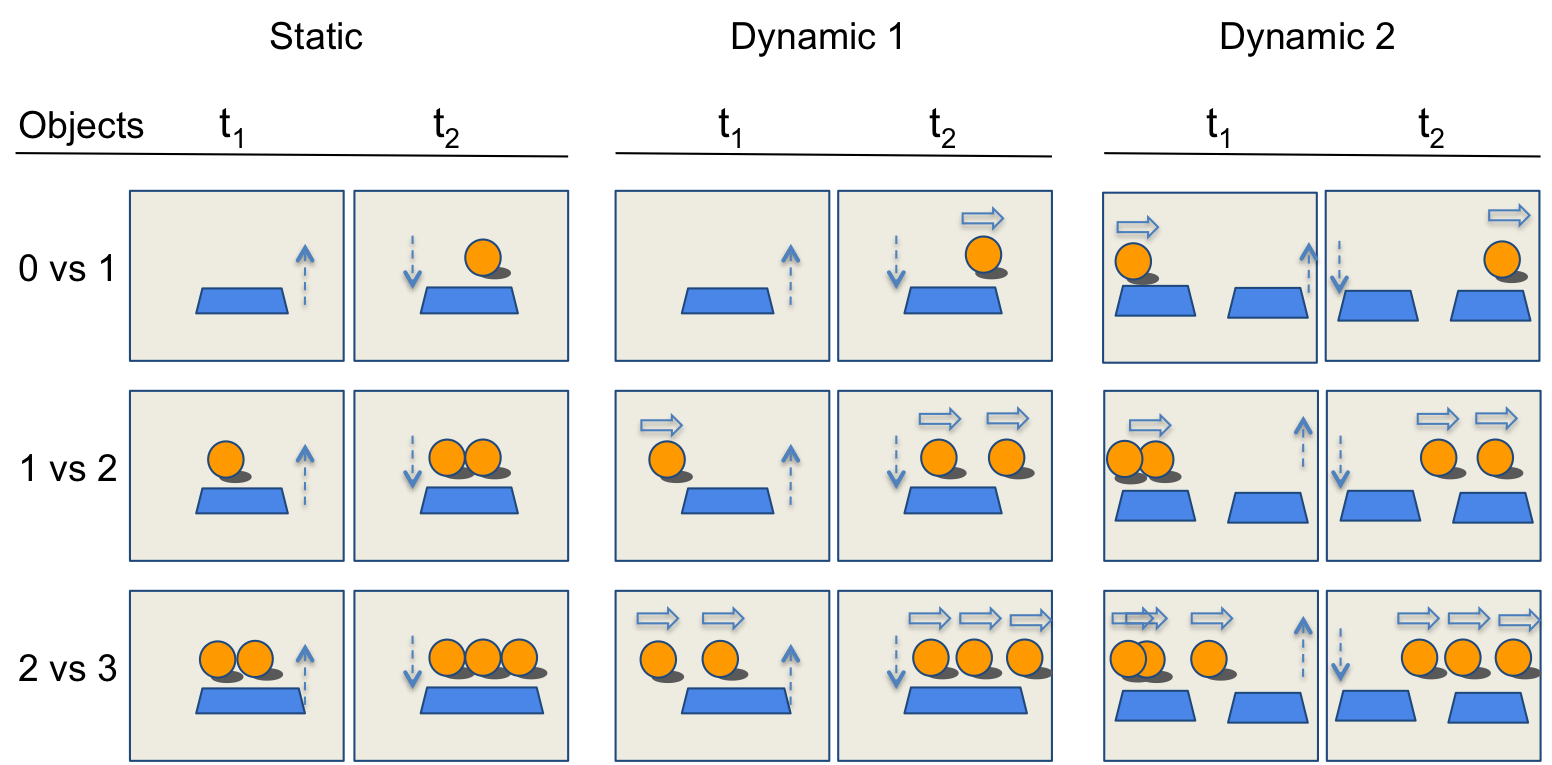
In total, for each block, the test set consists in 3.6K clips (200 clips for each of the 18 conditions). The dev set is much smaller, and only there to allow tuning of the plausibility function, but not for detailed model comparison (12 clips per condition, 216 total). The files in the dev set are provided with metadata and the evaluation code. The test set is just provided with raw videos (RGBD), but no metadata nor evaluation code.
Evaluation metric
The system requirements are that given a movie x, it must return a plausibility score P(x). Because the test movies are structured in N matched sets of positive and negative movies S_i = \{Pos^1_i .. Pos^{n_i}_i , Imp^1_i .. Imp^{n_i}_i\}, we derive two different metrics. The relative error rate L_R computes a score within each set. It requires only that within a set, the positive movies are more plausible than negative movies.
L_{R}=\frac{1}{N}\sum_{i}{\mathbb{I}_{\sum_{j}P(Pos_{i}^{j}) < \sum_{j}P(Imp_{i}^{j})}}
The absolute error rate L_A requires that globally, the score of the positive movies is more positive than the score of the negative movies. It is computed as:
L_{A}=1-AUC(\{i,j; P(Pos_{i}^{j})\}, \{i,j; P(Imp_{i}^{j})\})
Where AUC is the Area Under the ROC Curve, which plots the true positive rate against the false positive rate at various threshold settings.
Human and baseline results
Here are the baselines results and human performance (evaluated through Amazon Mechanical Turk) on this test for blocks O1, O2 and O3 of the Benchmark.
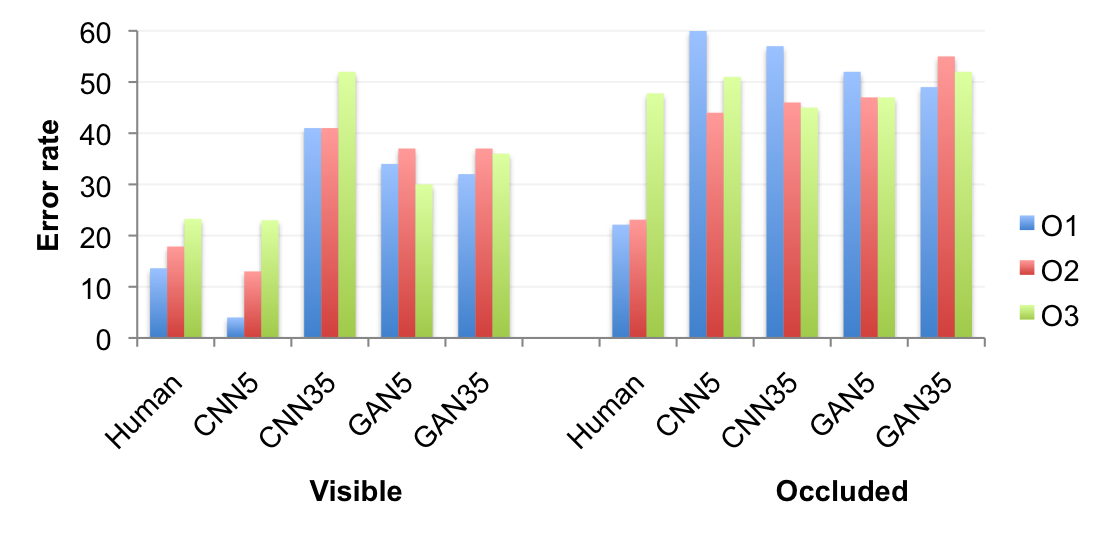
The source code for the baseline systems can be found here: https://github.com/rronan/IntPhys-Baselines.